Mouse Collision with Inclined Sprite
by Agustin Rosso
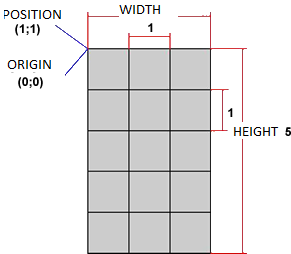
When creating a rectangle, you need 4 pieces of data:
- the X position of the sprite on the screen,
- the Y position of the sprite on the screen,
- the height of the sprite,
- the width of the sprite.
Rectangle _sprite = new Rectangle(1, 1, 3, 5); |
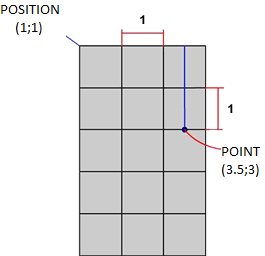
That way, it is very easy to determine when a Rectangle intersects with a point.
We create a new rectangle with the position of the point and we make the intersection:
Rectangle _point = new Rectangle(3.5f, 3, 1, 1); bool _result = _sprite.Intersects(_point); |
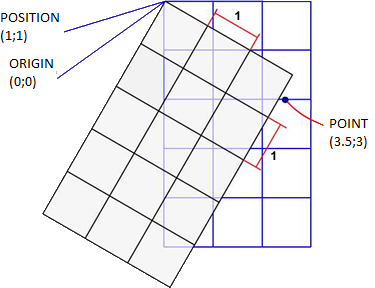
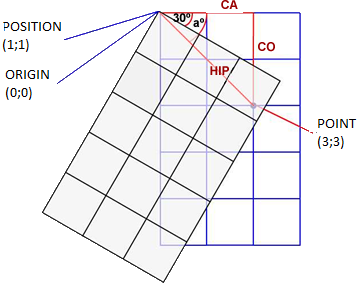
The problem rises when making the rectangle of an inclined sprite. We can't make it as we did before, since it would include the blue rectangle (in the graphics).
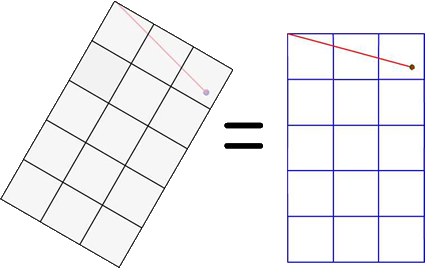
The solution of this problem is to move the point to the position it would have if the sprite wasn't inclined. That way, we can check the intersection as we used to.
In this case, it is necessary to have:
- the angle of the inclined sprite,
- the point in which the intersection corroborates.
First, we need to make sure that the inclination angle has the "point" inrespect with the origin of the sprite. We'll do that with the following formula:
a =cta(co/ca)
With:
a =cta(co/ca)
With:
- co (opposite egment) = y (adjacent segment)
- ca = x
- cta (cotangent)
- a = cta(2/2) = 45°
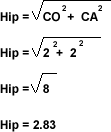
If CA is negative, then we must assign that sign to the result of the hypotenuse.
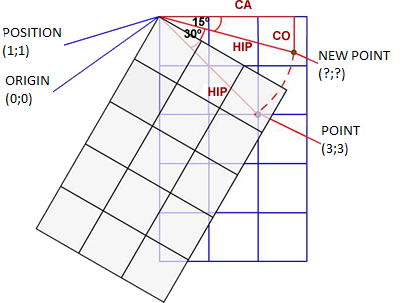
The next step is to calculate the position of the "point" inclined in 30°, i.e. the position the point would occupy hadn't the sprite been inclined.
The next step is to calculate the position of the "point" inclined in 30°, i.e. the position the point would occupy hadn't the sprite been inclined.
As it was calculated before, the real angle between the point and the origin is 15°.
Finally, to calculate the new point, we need to find the value of Ca and Co with the following formula:
New point = (3.73;1.73)
Other example:
Finally, to calculate the new point, we need to find the value of Ca and Co with the following formula:
- Co = sin(a°) * Hip -> Co = sin(15°) * 2.83 -> Co = 0.73
- Ca = cos(a°) * Hip -> Ca = cos(15°) * 2.83 -> Ca = 2.73
New point = (3.73;1.73)
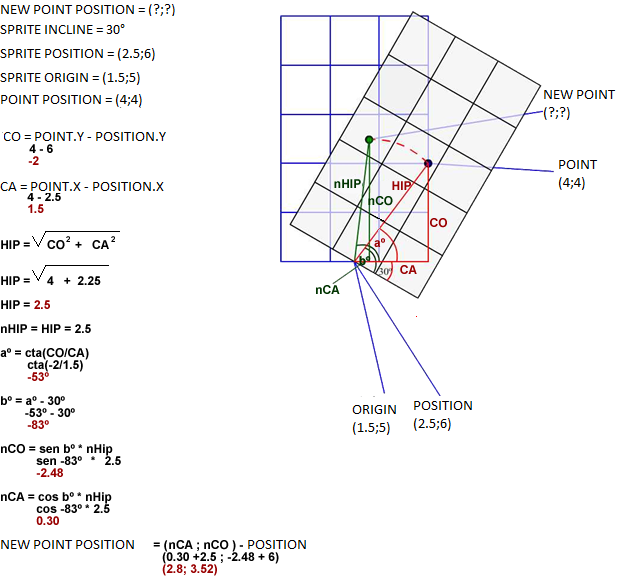
Other example: